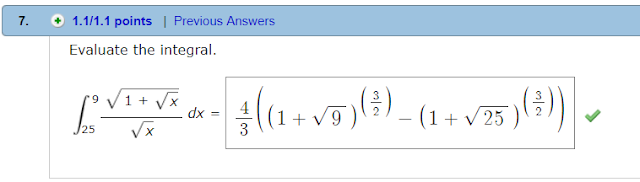Remember in the Webassign section there are other answer sets just not explanations!
This type of problem is best described as a square cylinder centered at the origin. The problem gives that the cross-sections are square so x^2 is equal to the area of any given cross-section. However, they note the side length in terms of radius so you need to multiplied by two. So 2x represents one length of the square and 4x^2 the area of the corresponding cross-section. Now because the base is a circle, the cross-sections will change depending on how close to the origin you are because of this you need to find an equation of x to represent the length of a side. In this case, the radius is largest (3 units) at the origin and smallest at plus of minus three units from the origin (0 units). You need to consider how as you travel across the x-axis of the circular base how y is affected.
Once you do this you can devise that 4(9-x^2) is the formula.
From here, you need to remember you placed the cylinder on the origin. As a result, the bounds of the integral are 3 to -3. The volume of the cylinder is simply just the function.
This problem is similar to first. However, the shape is a circular dome centered at the origin and the cross-section is a semi-circle. If you have forgotten the semi-circle area formula, you can just think of half of a circle's area (.5 pi R^2). Now, like the problem before, you need to find an equation to explain the relationship between how the area of the semi-circle changes as the x changes. This will expression will take the place of R. In this case, the given radius is 3 meaning at zero the largest radius of the cross-section of the semi-circle is 3 and whatever x is the radius will be smaller. Finally combine this information with the area of semi-circle formula.
Now, same are the prior question. The integral's bounds are from 4 to -4 because it's centered on the origin and the formula is just the integral of A(x).
Small Note: To integrate, remember you can use the property of symmetry to eliminate the pi/2 to just pi. Just remember to change the bounds from -4 to 0.
For this problem, place the given interval in for the bounds. Next remember the formula for a revolved volume is the integral of pi[f(x)]^2 bounded by a and b. As a result, the f(y) put in place of f(x) in the formula. From here, you can simplify and eliminate the square from the formula and 1/2 exponent of f(y) (or a square-root).
Small Note: Remember to add dy not dx for the integral formula.
Now integrate, remember the integral of e^x is still e^x but e^7x integrates to (1/7)e^(7x). Also remember, that e^1=e and e^0=1.
Small Note: The last part you can round up and personally used a calculator.
For this problem, you have to find the bounds by finding where f(x) and g(x) are equivalent. You can do this by setting them equal to each other. Next, you need to find which function is on top. You can do this by graphing or with a test point. The function that is larger (or on top) is having its full area to the x axis subtracted from the g(x). Think of a donuts, f(x) is the outside circle and g(x) is the inside circle. As a result, you need to subtract g(x) from f(x) but the formula is similar to the prior problem. V still equals the integral of (pi R^2) but R isn't the complete distance to the x axis. As a result, the formula looks more like (pi (f(x)^2 - g(x)^2)).
Next, solve the integral. Remember the property of sums so you can pull apart the integral into separate simpler integrals to be added together at the end.
For this problem, try to think of c as a change in where the x-axis is in terms of y. So if c is positive, the cross-section of F(x) gets smaller. If c is negative, then the cross-section gets bigger. As a result, F(x)-c is equal to the radius of the equation (pi R^2). This is similar to the prior problem.
As the problem says, use the equation from the prior problem. The interval is the bounds of the integral. Integrate using u-sub.
For this problem, remember 1/sqrt(x) is equal to x^-.5. This is d-u when 1+sqrt(x) is u. Then integrate as normal.
